Problems
- A hospital dietitian must find the cheapest combination of two products, A and B, that contain at least 0.5 milligrams of thiamine and at least 600 calories. Each ounce of A contains 0.12 milligrams of thiamine and 100 calories; while each ounce of B contains 0.08 milligrams of thiamine and 150 calories. If the cost of each food is $ 10 per ounce, how many ounces of each should be combined?
- A bus that makes the Pereira-Armenia route offers seats for smokers at the price of 12,000 pesos and non-smokers at the price of 9,000 pesos. The non-smoker is allowed to carry 50 kg of weight and the smoker 20 kg. If the bus has 90 seats and admits luggage of up to 3,000 kg. What should be the company's seat offer for each type of passenger? , in order to optimize profit? In addition, it should be considered that by company policies, a minimum of 10 non-smoking seats must be offered.
- The Versatech Corporation will produce three new products. At this time, five of its plants have excess production capacity. The respective unit cost of manufacturing the first product will be: $ 31, $ 29 $ 32, $ 28 and $ 29 in plants 1, 2, 3, 4 and 5. The unit cost of manufacturing the second prod,uct will be $ 45, $ 41, $ 46, $ 42 and $ 43 in plants 1, 2, 3,4 and 5 respectively, and for the third product it will be $ 38, $ 35 and $ 40 in plants 1,2 and 3 but plants 4 and 5 cannot manufacture this product. The sales forecasts indicate that the daily production should be 600, 1000 and 800 units of products 1, 2 and 3, respectively. Plants 1, 2, 3, 4 and 5 have capacities to produce 400, 600, 400, 600 and 1000 units per day, regardless of the product or combination of products. Suppose that any plant that has the capacity and the ability to manufacture them will be able to produce any number of products and with any combination.
Development
1. Best recipe
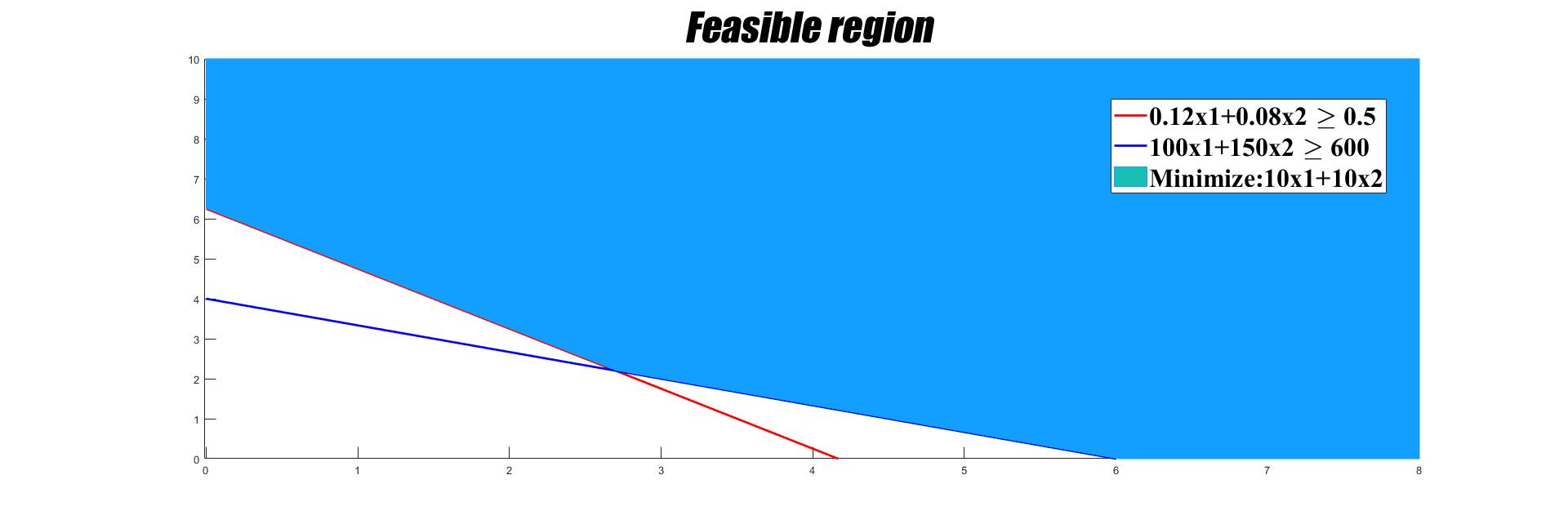
A hospital dietitian must find the cheapest combination of two products, A and B, that contain at least 0.5 milligrams of thiamine and at least 600 calories. Each ounce of A contains 0.12 milligrams of thiamine and 100 calories; while each ounce of B contains 0.08 milligrams of thiamine and 150 calories. If the cost of each food is $ 10 per ounce, how many ounces of each should be combined?
a. Make a table from the data of the problem(You should edit the table, after that you can rectify just click on the button below the table)
| Product | Thiamine(mg) | Calories | Cost $ |
|---|---|---|---|
| A | 0 | 0 | 0 |
| B | 0 | 0 | 0 |
| Conditions | 0 | 0 |
b. Objective Function and constraints from the data of the problem
\begin{equation} Minimize:10X_{1}+10X_{2} \end{equation}
~ Subject to
\begin{equation} 0.12X_{1}+0.08X_{2}\geqslant 0.5 \end{equation} \begin{equation} 100X_{1}+150X_{2}\geqslant 600 \end{equation} \begin{equation} X_{1},X_{2}\geqslant 0 \end{equation}
Now you should define de vector(Objective Function and constraints) and the matrix and vector (Subject to).
Note:The values of A_ub and b_ub must be set negative when the inequality is not of the form ≤
A_ub=[[ 0 , 0 ],[ 0 , 0 ],[ 0 , 0 ],[ 0 , 0 ]]
b_ub=[ 0 , 0 , 0 , 0 ]
Now you should to code below for showing the result and best option for this problem
2. Best seats between smokers-non-smokers
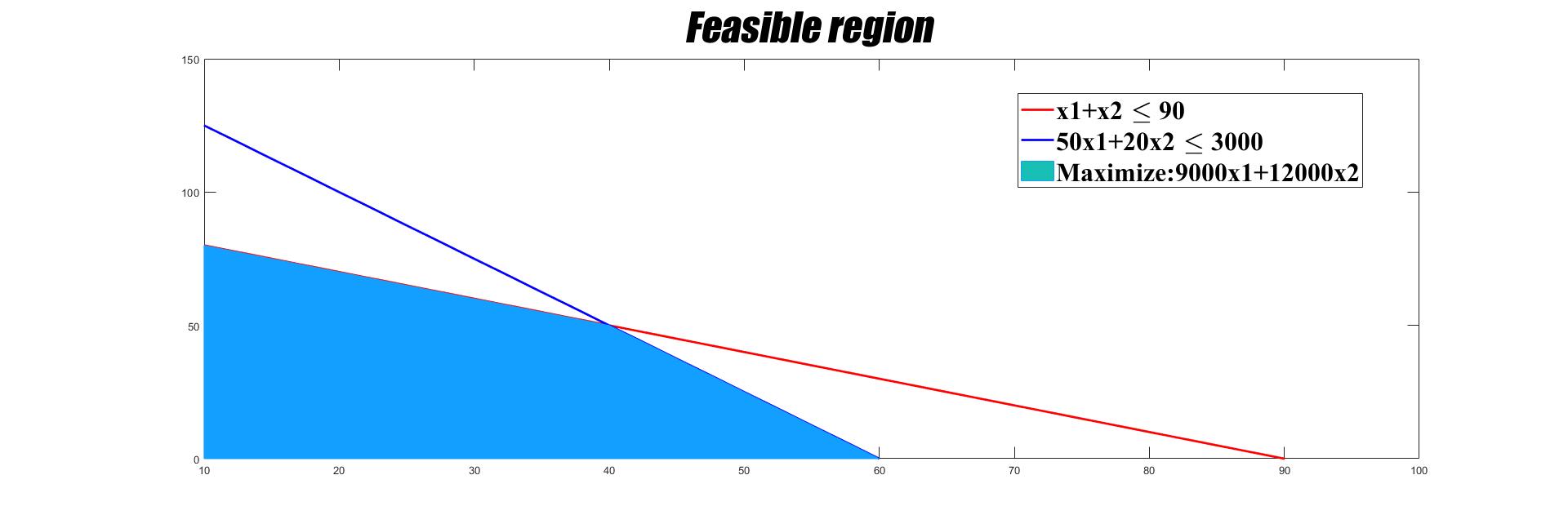
A bus that makes the Pereira-Armenia route offers seats for smokers at the price of 12,000 pesos and non-smokers at the price of 9,000 pesos. The non-smoker is allowed to carry 50 kg of weight and the smoker 20 kg. If the bus has 90 seats and admits luggage of up to 3,000 kg. What should be the company's seat offer for each type of passenger? , in order to optimize profit? In addition, it should be considered that by company policies, a minimum of 10 non-smoking seats must be offered.
a. Make a table from the data of the problem(You should edit the table, after that you can rectify just click on the button below the table)
| Passenger | Weight(kg) | Cost $ |
|---|---|---|
| Smoker | 0 | 0 |
| Non smoker | 0 | 0 |
| Conditions | 0 |
b. Objective Function and constraints from the data of the problem
\begin{equation} Maximize:9000X_{1}+12000X_{2} \end{equation}
~ Subject to
\begin{equation} X_{1}+X_{2}\leqslant 90 \end{equation} \begin{equation} 50X_{1}+20X_{2}\leqslant 3000 \end{equation} \begin{equation} X_{1}\geqslant 10 \end{equation} \begin{equation} X_{1},X_{2}\geqslant 0 \end{equation}
Now you should define de vector(Objective Function and constraints) and the matrix and vector (Subject to).
1. Note:The values of A_ub and b_ub must be set negative when the inequality is not of the form ≤
2. Note: when maximizing, change the signs of the c vector coefficient
A_ub=[[ 0 , 0 ],[ 0 , 0 ],[ 0 , 0 ],[ 0 , 0 ],[ 0 , 0 ]]
b_ub=[ 0 , 0 , 0 , 0 , 0 ]
Now you should to code below for showing the result and best option for this problem
3. Best production
The Versatech Corporation will produce three new products. At this time, five of its plants have excess production capacity. The respective unit cost of manufacturing the first product will be: $ 31, $ 29 $ 32, $ 28 and $ 29 in plants 1, 2, 3, 4 and 5. The unit cost of manufacturing the second prod,uct will be $ 45, $ 41, $ 46, $ 42 and $ 43 in plants 1, 2, 3,4 and 5 respectively, and for the third product it will be $ 38, $ 35 and $ 40 in plants 1,2 and 3 but plants 4 and 5 cannot manufacture this product. The sales forecasts indicate that the daily production should be 600, 1000 and 800 units of products 1, 2 and 3, respectively. Plants 1, 2, 3, 4 and 5 have capacities to produce 400, 600, 400, 600 and 1000 units per day, regardless of the product or combination of products. Suppose that any plant that has the capacity and the ability to manufacture them will be able to produce any number of products and with any combination.
a. Make a graph from the data of the problem
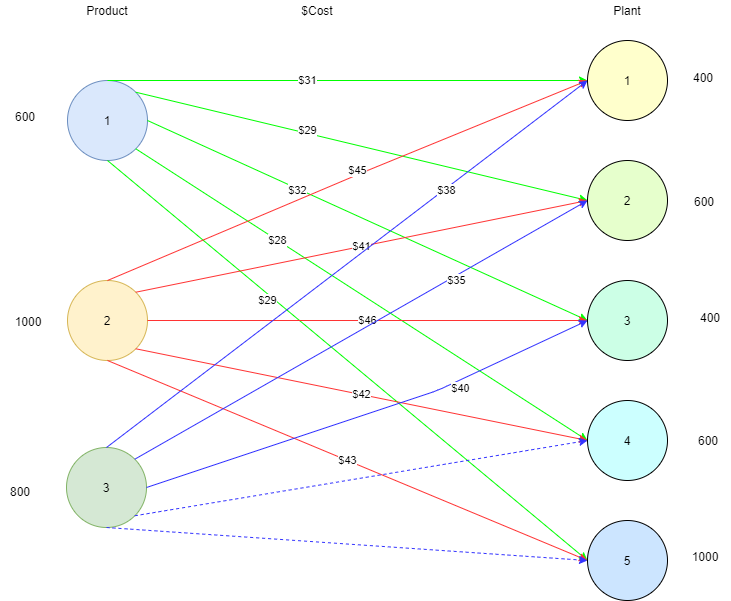
| Plants | P 1 | P 2 | P 3 | Quantity |
|---|---|---|---|---|
| Plant 1 | 31 | 45 | 38 | 400 |
| Plant 2 | 29 | 41 | 35 | 600 |
| Plant 3 | 32 | 46 | 40 | 400 |
| Plant 4 | 28 | 42 | 0 | 600 |
| Plant 5 | 29 | 43 | 0 | 1000 |
| Dairy produce | 600 | 1000 | 800 |
Since the demand and supply are not balanced, a fictitious product must be created , which helps to compensate this for solving this problem.
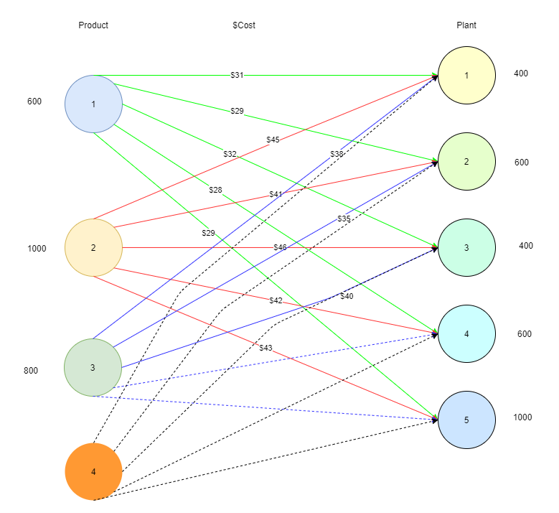
| Plants | P 1 | P 2 | P 3 | P 4(*) | Quantity |
|---|---|---|---|---|---|
| Plant 1 | 31 | 45 | 38 | 0 | 400 |
| Plant 2 | 29 | 41 | 35 | 0 | 600 |
| Plant 3 | 32 | 46 | 40 | 0 | 400 |
| Plant 4 | 28 | 42 | 0 | 0 | 600 |
| Plant 5 | 29 | 43 | 0 | 0 | 1000 |
| Dairy produce | 600 | 1000 | 800 | 600 |
b. Objective Function and constraints \begin{equation} Minimize:31X_{11}+45X_{12}+38X_{13}+29X_{21}+41X_{22}+35X_{23}+32X_{31}+46X_{32}+40X_{33}+28X_{41}+42X_{42}+29X_{51}+43X_{52} \end{equation}
~ Subject to
\begin{equation} X_{ij}\geqslant 0 ,X_{ij} \epsilon \mathbb{Z} \end{equation}
Now you should define de vector(Objective Function and constraints) and the matrix and vector (Subject to).
1. Note:The values of A_ub and b_ub must be set negative when the inequality is not of the form ≤
2. Note: when maximizing, change the signs of the c vector coefficient
A_ub=[
[ 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 ],
[ 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 ],
[ 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 ],
[ 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 ],
[ 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 ]
]
b_ub=[ 0 , 0 , 0 , 0 , 0 ]
A_eq=[
[ 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 ],
[ 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 ],
[ 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 ]
]
b_eq=[ 0 , 0 , 0 ]