Introduction
This is a module oriented to the analysis of electrical circuits with phasors. It starts from a presentation of the complex algebra necessary for the operations demanded by the circuit and from the presentation of the concept of impedance as a complex relationship between voltages and currents in the frequency domain.
The circuit, somewhat more general than the previous one, has components such as resistors, inductors, capacitors, and power supplies. From these elements, we will move to the frequency domain, adopting the concepts of phasor and impedance. To do this it will be important to consider complex algebra procedures that are worked in the first part.
Once the circuit has passed to the frequency domain and, therefore, it is expressed in complex quantities, the circuit is analyzed using, in this case, Kirchhoff's Law of Currents (KLC), through nodal analysis, to get the circuit voltages.
It is also important to highlight the notions of amplitude, phase, frequency, phase angle between two signals of the same frequency and the respective egraphic presentation. Finally, Python will be used as a tool to facilitate the elaboration of the respective support or complement graphics in the circuit analysis.
Signal gap
Also known as the phase shift between two waves, it is the difference that exists between its two phases. Generally, this phase difference is measured at the same instant for the two waves, but not always in the same place. With the following Python code, a sinusoidal signal of amplitude 10 (blue signal) and a cosine signal of equal amplitude (red signal) are graphed.
From the graph above it is evident that the signals are very similar as their period, frequency and amplitude are same, to view the red represented as a sinusoidal signal must have a shift of only 90 degrees, so we can deduce that cosine signal is a sinusoidal signal shifted 90 degrees.
Phasor representation
Phasor is defined as a complex number that represents the amplitude and phase of a sinusoidal signal. Complex numbers are those that are composed of the sum of a real number and an imaginary number, it is written in the form:
\begin{equation} Z= x + j y = R \angle \Phi \end{equation}
Where:
- Z: Impedance
- x: real component
- y: imaginary component
- j: Refers to the imaginary unit
- R: phasor amplitude
- Phi: Refers to the phasor angle
To represent a complex number in the Cartesian plane, the abscissa or x-axis will be taken to represent the real numbers and the ordinate or y-axis to represent the complex numbers.
Example:
- Represent the phasor 2 + 2j in a plane, considering that the imaginary axis is vertical and the real axis is horizontal.
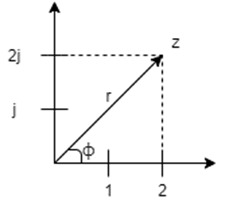
- Represent the signals of point 2 (this module), in polar form, by using python and make their representation in the complex plane.
In the code that is presented below for the solution of the example, it must be taken into account that the value of the phasor is given by python, it is given the vector of rectangular shape and the program provides the solution in magnitude and angle.
Phasor conversion
To perform the conversion of the phasor between its rectangular shape and its polar shape, it must be remembered that the handling of the phasor is usually reduced to its polar shape (magnitude and angle).
The magnitude of the phasor is obtained as the square root of the real term squared plus the imaginary term squared; the phase, on the other hand, is obtained by finding the inverse tangent (arctan) of the imaginary part value divided by its real part.
- In more formal terms where $$z = x+jy$$
\begin{eqnarray} r=\sqrt{xˆ2+yˆ2} \end{eqnarray} \begin{eqnarray} \Phi = ArcTan \frac{y}{x} \end{eqnarray}
- Similarly, for the inverse conversion from polar to rectangular coordinates, the following transformation is applied:
$$x=r\cdot cos(\Phi)$$
$$y=r\cdot sin(\Phi)$$
Operations between complex numbers
Adition
To perform the addition, like terms are operated; that is, the real and imaginary parts are added independently. E.g.
$$z1=3+2j$$ $$z2=5+7j$$ $$z3=z1+z2=(3+5)+(2+7)j$$ $$z3=8+9j$$
Substraction
Subtraction is handled similarly to addition; real and imaginary parts are subtracted independently. E.g.
$$z1=3+2j$$ $$z2=5+7j$$ $$z3=z1-z2=(3-5)+(2-7)j$$ $$z3=-2-5j$$
Product
To perform multiplication polar forms of the complex factors are used so that the magnitude of the product is the product of the magnitudes and, phase of the product is the sum of its phases. E.g.
$$z1=3+2j=\sqrt{13}\angle 33.69$$ $$z2=5+7j=\sqrt{74}\angle 54.46$$ $$z3=z1\cdot z2=3,6\cdot 8.6 \angle (33.69+54.46)$$ $$z3=31.02 \angle 88.15=1+31j$$
Division
Division is handled similarly to the product of complexes; polar forms of the complex factors are used so that the magnitude of the ratio is the ratio of the magnitudes and phase of the quotient is the subtraction of the phases. E.g.
$$z1=3+2j=3.606\angle 33.69$$ $$z2=5+7j=8.602\angle 54.46$$ $$z3=z1 / z2=\frac{3,6}{8.6} \angle (33.69-54.46)$$ $$z3=0.4191 \angle -20.77 = 0.3919-0.1486j$$
